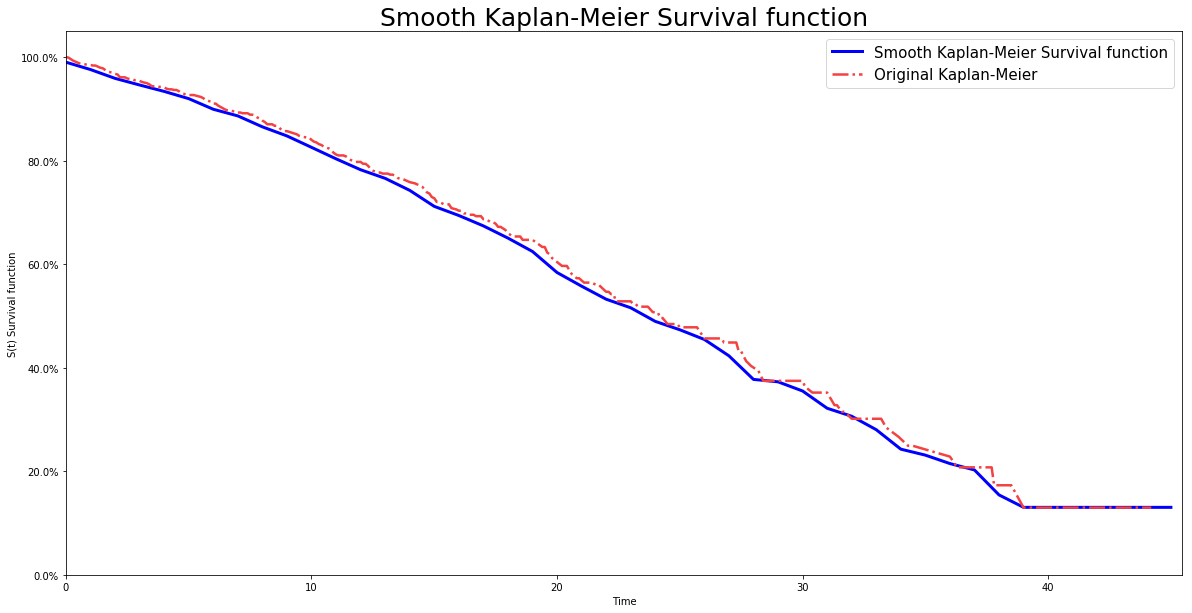


Smooth Kaplan Meier model

Smooth Kaplan Meier model is computed by using kernel smoothing to obtained a smooth estimator.

---

Instance

To create an instance, use pysurvival.models.non_parametric.SmoothKaplanMeierModel.

---

Attributes

• cumulative_hazard: array-like -- representation of the cumulative hazard function of the model
• hazard: array-like -- representation of the hazard function of the model
• survival: array-like -- representation of the Survival function of the model
• times: array-like -- representation of the time axis of the model
• time_buckets: array-like -- representation of the time axis of the model using time bins, which are represented by $[ t_{k-1}, t_k )$

---

Methods

__init__ - Initialize the estimator

SmoothKaplanMeierModel(bandwidth=0.1, kernel='normal')

Parameters:

• bandwidth: double (default=0.1) -- controls the degree of the smoothing. The smaller it is the closer to the original KM the function will be, but it will increase the computation time. If it is very large, the resulting model will be smoother than the estimator of KM, but it will stop being as accurate.

• kernel: str (default='normal') -- defines the type of kernel the model will be using. Here are the possible options:

  • Uniform: $f(x) = 0$ if $|x|<1$ else $f(x) = 0.5$
  • Epanechnikov: $f(x) = 0$ if $|x| \leq 1$ else $f(x) = 0.75 \cdot (1 - x^2 )$
  • Normal: $f(x) = \exp( -x^2/2) / \sqrt{2 \cdot \pi}$
  • Biweight: $f(x) = 0$ if $|x| \leq 1$ else $f(x)=(15/16) \cdot (1-x^2)^2$
  • Triweight: $f(x) = 0$ if $|x| \leq 1$ else $f(x)=(35/32) \cdot (1-x^2)^3$
  • Cosine: $f(x) = 0$ if $|x| \leq 1$ else $f(x)=(\pi/4) \cdot \cos( \pi \cdot x/2. )$

fit - Fit the estimator based on the given parameters

fit(T,  E, weights = None, alpha=0.05)

Parameters:

• T : array-like -- target values describing the time when the event of interest or censoring occurred.

• E : array-like -- values that indicate if the event of interest occurred i.e.: E[i]=1 corresponds to an event, and E[i] = 0 means censoring, for all i.

• weights : array-like (default = None) -- array of weights that are assigned to individual samples. If not provided, then each sample is given a unit weight.

• alpha: float (default = 0.05) -- confidence level

Returns:

• self : object

predict_density - Predicts the probability density function $p(t)$ at a specified time t

predict_density(t)

Parameters:

• t: double -- time at which the prediction should be performed.

Returns:

• density: double -- prediction of the probability density function at t

predict_hazard - Predicts the hazard function $h(t)$ at a specified time t

predict_hazard(t)

Parameters:

• t: double -- time at which the prediction should be performed.

Returns:

• hazard: double -- prediction of the hazard function at t

predict_survival - Predicts the survival function $S(t)$ at a specified time t

predict_survival(t)

Parameters:

• t: double -- time at which the prediction should be performed.

Returns:

• survival: double -- prediction of the survival function at t

---

Example

# Importing modules
import numpy as np
from matplotlib import pyplot as plt
from pysurvival.models.non_parametric import SmoothKaplanMeierModel
from pysurvival.utils.display import display_non_parametric
# %matplotlib inline #Uncomment when using Jupyter 

# Generating random times and event indicators 
T = np.round(np.abs(np.random.normal(10, 10, 1000)), 1)
E = np.random.binomial(1, 0.3, 1000)

# Initializing the SmoothKaplanMeierModel
skm_model = SmoothKaplanMeierModel(bandwidth=1., kernel='Cosine')

# Fitting the model and display the survival function and confidence intervals
skm_model.fit(T, E, alpha=0.95)

# Displaying the survival function and confidence intervals
display_non_parametric(skm_model)

Figure 1 - Representation of the Smooth Kaplan Meier Survival function