

Simulation models

PySurvival can generate random survival times based on the most commonly used distributions such as:

• Exponential
• Weibull
• Gompertz
• Log-Logistic
• Lognormal

---

Instance

To create an instance, use pysurvival.models.simulations.SimulationModel.

---

Attributes

• alpha: double -- the scale parameter
• beta: double -- the shape parameter
• censored_parameter: double -- coefficient used to calculate the censored distribution.
• risk_type: string -- Defines the type of risk function.
• risk_parameter: double -- scaling coefficient of the risk score
• survival_distribution: string -- Defines a known survival distribution.
• times: array-like -- representation of the time axis of the model
• time_buckets: array-like -- representation of the time axis of the model using time bins, which are represented by $[ t_{k-1}, t_k )$

---

API

__init__ - Initialization

SimulationModel( survival_distribution = 'exponential', risk_type = 'linear',
                 censored_parameter = 1., alpha = 1, beta = 1., bins = 100,
                 risk_parameter = 1.)

Parameters:

• survival_distribution: string (default = 'exponential') -- Defines a known survival distribution. The available distributions are:

  • Exponential
  • Weibull
  • Gompertz
  • Log-Logistic
  • Log-Normal

• risk_type: string (default='linear') -- Defines the type of risk function: - Linear - Square - Gaussian

• censored_parameter: double (default = 1.) -- Coefficient used to calculate the censored distribution. This distribution is a normal such that N(loc=censored_parameter, scale=5)

• alpha: double (default = 1.) -- the scale parameter

• beta: double (default = 1.) -- the shape parameter

• bins: int (default=100) -- the number of bins of the time axis

• risk_parameter: double (default = 1.) -- Scaling coefficient for the risk score which can be written as follow:

  • linear: $r(x) = \exp(x \cdot \omega)$
  • square: $r(x) = \exp( \text{risk_parameter} *(x \cdot \omega)^2)$
  • gaussian: $r(x) = \exp \left( e^{-(x \cdot \omega)^2*\text{risk_parameter}} \right)$

generate_data - Generating a dataset of simulated survival times from a given distribution through the hazard function using the Cox model

generate_data(num_samples = 100, num_features = 3, feature_weights=None)

Parameters:

• num_samples: int (default=100) -- Number of samples to generate

• num_features: int (default=3) -- Number of features to generate

• feature_weights: array-like (default=None) -- list of the coefficients of the underlying Cox-Model. The features linked to each coefficient are generated from random distribution from the following list:

  • binomial
  • chisquare
  • exponential
  • gamma
  • normal
  • uniform
  • laplace

  If None then feature_weights = [1.]*num_features

Returns:

• dataset: pandas.DataFrame -- dataset of simulated survival times, event status and features

predict_hazard - Predicts the hazard function $h(t, x)$

predict_hazard(x, t = None)

Parameters:

• x : array-like -- input samples; where the rows correspond to an individual sample and the columns represent the features (shape=[n_samples, n_features]). x should not be standardized before, the model will take care of it

• t: double (default=None) -- time at which the prediction should be performed. If None, then it returns the function for all available t.

Returns:

• hazard: numpy.ndarray -- array-like representing the prediction of the hazard function

predict_risk - Predicts the risk score $r(x)$

predict_risk(x)

Parameters:

• x : array-like -- input samples; where the rows correspond to an individual sample and the columns represent the features (shape=[n_samples, n_features]). x should not be standardized before, the model will take care of it

Returns:

• risk_score: numpy.ndarray -- array-like representing the prediction of the risk score

predict_survival - Predicts the survival function $S(t, x)$

predict_survival(x, t = None)

Parameters:

• x : array-like -- input samples; where the rows correspond to an individual sample and the columns represent the features (shape=[n_samples, n_features]). x should not be standardized before, the model will take care of it

• t: double (default=None) -- time at which the prediction should be performed. If None, then return the function for all available t.

Returns:

• survival: numpy.ndarray -- array-like representing the prediction of the survival function

---

Example

Let's now see how to generate a dataset designed for survival analysis.

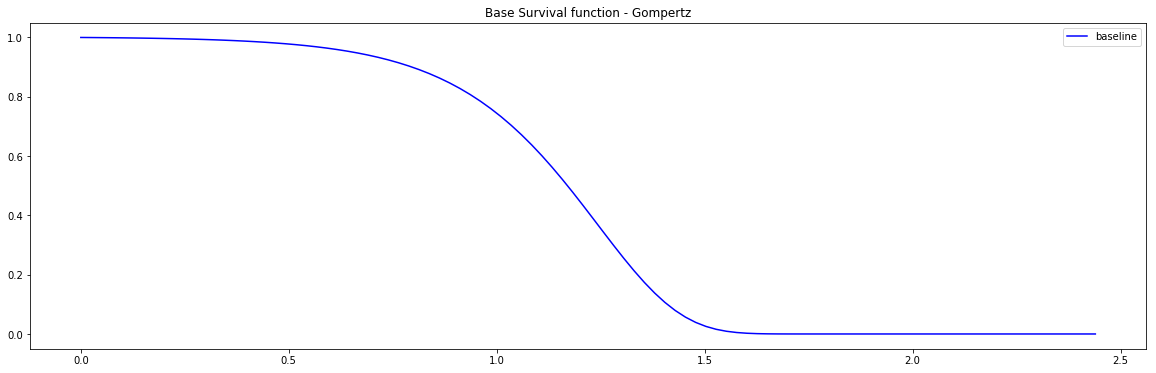
import pandas as pd
from pysurvival.models.simulations import SimulationModel
%pylab inline

# Initializing the simulation model
sim = SimulationModel( survival_distribution = 'gompertz',
                       risk_type = 'linear',
                       censored_parameter = 5.0,
                       alpha = 0.01,
                       beta = 5., )

# Generating N Random samples
N = 1000
dataset = sim.generate_data(num_samples = N, num_features=5)

# Showing a few data-points
dataset.head(2)

We can now see an overview of the data:

x_1	x_2	x_3	x_4	x_5	time	event
3.956896	124.0	0.018274	57.480199	-5.42258	0.024329	1.0
4.106100	117.0	0.111276	51.770875	4.105588	0.175530	1.0

PySurvival also displays the Base Survival function of the Simulation model:

from pysurvival.utils.display import display_baseline_simulations
display_baseline_simulations(sim, figure_size=(20, 6))

Figure 1 - Base Survival function of the Simulation model