

Cox Proportional Hazard model

The Cox Proportional Hazard model (CoxPH) is a semi-parametric model that focuses on modeling the hazard function $h(t, x_i)$ , by assuming that its time component $\lambda_0(t)$ and feature component $\eta(\vec{x_i})$ are proportional such that: $\begin{equation*} h(t, \vec{x_i}) = h_0(t)\eta(\vec{x_i}) \end{equation*}$ with:

$h_0(t)$ , is the baseline function, which is usually not specified.
$\eta(\vec{x_i})$ , is the risk function usually expressed via a linear representation such that $\eta(\vec{x_i}) = \exp \left( \sum_{j=1}^p x^i_j\omega_j \right)$ . $\omega_j$ are the coefficients to determine

Instance

To create an instance, use pysurvival.models.semi_parametric.CoxPHModel.

Attributes

baseline_hazard: array-like -- values of the hazard function when $x \equiv 0$
baseline_survival: array-like -- values of the survival function when $x \equiv 0$
summary: pandas.DataFrame -- summary of the modeling results
times: array-like -- representation of the time axis of the model
time_buckets: array-like -- representation of the time axis of the model using time bins, which are represented by $[ t_{k-1}, t_k )$
weights: array-like -- model coefficients

Methods

fit - Fit the estimator based on the given parameters

fit(X, T, E, init_method='glorot_normal', lr = 1e-2, max_iter = 100, l2_reg = 1e-4, alpha = 0.95, tol = 1e-3, epsilon=1e-9, verbose = True, display_loss=True)

Parameters:

X : array-like -- input samples; where the rows correspond to an individual sample and the columns represent the features (shape=[n_samples, n_features]).
T : array-like -- target values describing the time when the event of interest or censoring occurred.
E : array-like -- values that indicate if the event of interest occurred i.e.: E[i]=1 corresponds to an event, and E[i] = 0 means censoring, for all i.
init_method : str (default = 'glorot_uniform') -- initialization method to use. Here are the possible options:
- glorot_uniform: Glorot/Xavier uniform initializer
- he_uniform: He uniform variance scaling initializer
- uniform: Initializing tensors with uniform (-1, 1) distribution
- glorot_normal: Glorot normal initializer,
- he_normal: He normal initializer.
- normal: Initializing tensors with standard normal distribution
- ones: Initializing tensors to 1
- zeros: Initializing tensors to 0
- orthogonal: Initializing tensors with a orthogonal matrix,
lr: float (default=1e-4) -- learning rate used in the optimization
max_iter: int (default=100) -- maximum number of iterations in the Newton optimization
l2_reg: float (default=1e-4) -- L2 regularization parameter for the model coefficients
alpha: float (default=0.95) -- confidence level
tol: float (default=1e-3) -- tolerance for stopping criteria
verbose: bool (default=True) -- whether or not producing detailed logging about the modeling

Returns:

self : object

predict_hazard - Predicts the hazard function $h(t, x)$

predict_hazard(x, t = None)

Parameters:

x : array-like -- input samples; where the rows correspond to an individual sample and the columns represent the features (shape=[n_samples, n_features]). x should not be standardized before, the model will take care of it
t: double (default=None) -- time at which the prediction should be performed. If None, then it returns the function for all available t.

Returns:

hazard: numpy.ndarray -- array-like representing the prediction of the hazard function

predict_risk - Predicts the risk score $r(x)$

predict_risk(x)

Parameters:

x : array-like -- input samples; where the rows correspond to an individual sample and the columns represent the features (shape=[n_samples, n_features]). x should not be standardized before, the model will take care of it

Returns:

risk_score: numpy.ndarray -- array-like representing the prediction of the risk score

predict_survival - Predicts the survival function $S(t, x)$

predict_survival(x, t = None)

Parameters:

x : array-like -- input samples; where the rows correspond to an individual sample and the columns represent the features (shape=[n_samples, n_features]). x should not be standardized before, the model will take care of it
t: double (default=None) -- time at which the prediction should be performed. If None, then return the function for all available t.

Returns:

survival: numpy.ndarray -- array-like representing the prediction of the survival function

Example

Let's now take a look at how to use the Cox PH model on a simulation dataset generated from a parametric model.

#### 1 - Importing packages
import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
from sklearn.model_selection import train_test_split
from pysurvival.models.simulations import SimulationModel
from pysurvival.models.semi_parametric import CoxPHModel
from pysurvival.utils.metrics import concordance_index
from pysurvival.utils.display import integrated_brier_score
#%pylab inline


#### 2 - Generating the dataset from a Log-Logistic parametric model
# Initializing the simulation model
sim = SimulationModel( survival_distribution = 'log-logistic',
                       risk_type = 'linear',
                       censored_parameter = 10.1,
                       alpha = 0.1, beta=3.2 )

# Generating N random samples 
N = 1000
dataset = sim.generate_data(num_samples = N, num_features = 4)

# Showing a few data-points 
dataset.head(2)

We can now see an overview of the data:

x_1	x_2	x_3	x_4	time	event
14.711368	123.0	0.022755	114.0	2.0	0.
14.584616	117.0	0.011464	116.0	9.0	0.

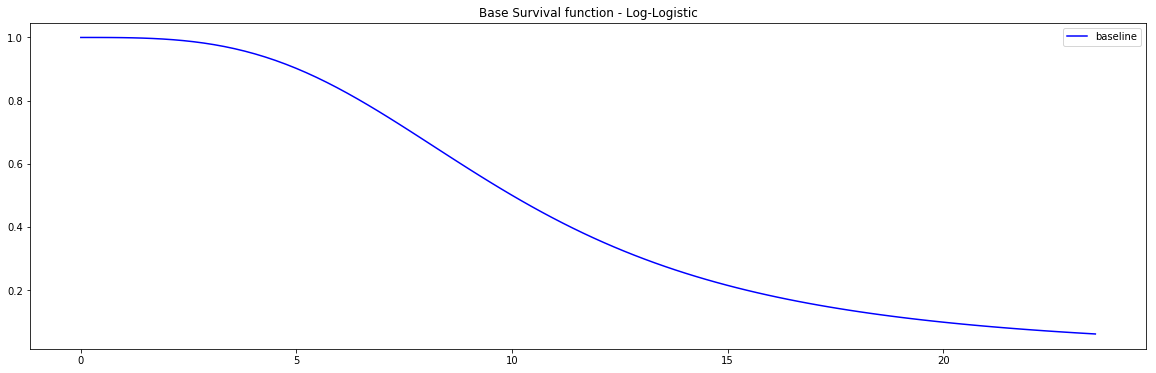
Pysurvival also displays the Base Survival function of the Simulation model:

from pysurvival.utils.display import display_baseline_simulations
display_baseline_simulations(sim, figure_size=(20, 6))

PySurvival - CoxPH model - Base Survival function of the Simulation model

Figure 1 - Base Survival function of the Simulation model

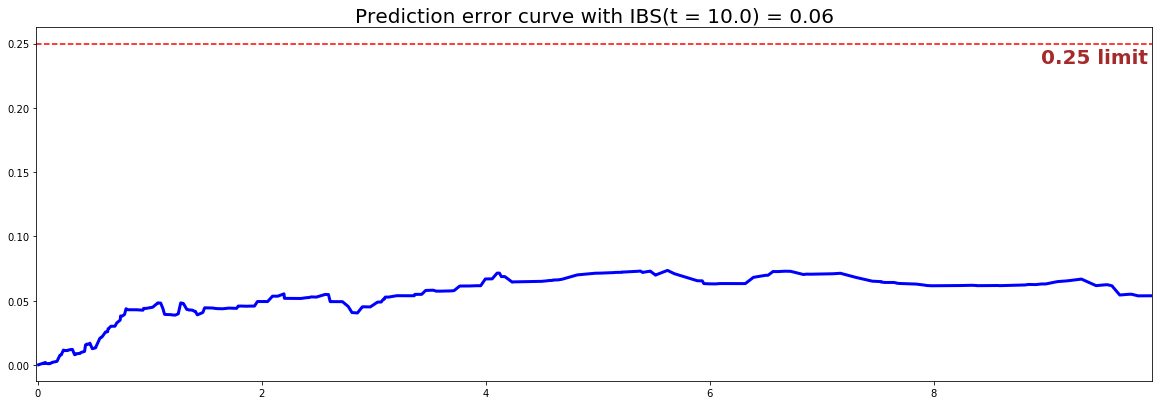
#### 3 - Creating the modeling dataset
# Defining the features
features = sim.features

# Building training and testing sets #
index_train, index_test = train_test_split( range(N), test_size = 0.2)
data_train = dataset.loc[index_train].reset_index( drop = True )
data_test  = dataset.loc[index_test].reset_index( drop = True )

# Creating the X, T and E input
X_train, X_test = data_train[features], data_test[features]
T_train, T_test = data_train['time'].values, data_test['time'].values
E_train, E_test = data_train['event'].values, data_test['event'].values


#### 4 - Creating an instance of the Cox PH model and fitting the data.
# Building the model
coxph = CoxPHModel()
coxph.fit(X_train, T_train, E_train, lr=0.5, l2_reg=1e-2, init_method='zeros')


#### 5 - Cross Validation / Model Performances
c_index = concordance_index(coxph, X_test, T_test, E_test) #0.92
print('C-index: {:.2f}'.format(c_index))

ibs = integrated_brier_score(coxph, X_test, T_test, E_test, t_max=10,
            figure_size=(20, 6.5) )
print('IBS: {:.2f}'.format(ibs))

We can see that the c-index is well above 0.5 and that the Prediction error curve is below the 0.25 limit, thus the model yields great performances.

PySurvival - CoxPH model - Prediction error curve

Figure 2 - Prediction error curve

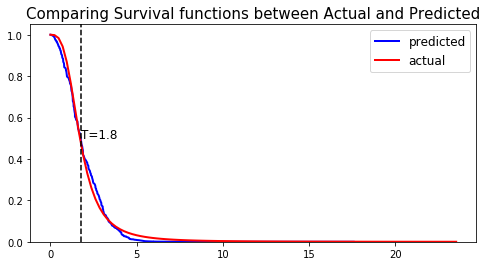
We can show this by randomly selecting datapoints and comparing the actual and predicted survival functions, computed by the simulation model and the CoxPH model respectively.

#### 6 - Comparing actual and predictions
# Initializing the figure
fig, ax = plt.subplots(figsize=(8, 4))

# Randomly extracting a data-point that experienced an event 
choices = np.argwhere((E_test==1.)&(T_test>=1)).flatten()
k = np.random.choice( choices, 1)[0]

# Saving the time of event
t = T_test[k]

# Computing the Survival function for all times t
predicted = coxph.predict_survival(X_test.values[k, :]).flatten()
actual = sim.predict_survival(X_test.values[k, :]).flatten()

# Displaying the functions
plt.plot(coxph.times, predicted, color='blue', label='predicted', lw=2)
plt.plot(sim.times, actual, color = 'red', label='actual', lw=2)

# Actual time
plt.axvline(x=t, color='black', ls ='--')
ax.annotate('T={:.1f}'.format(t), xy=(t, 0.5), xytext=(t, 0.5), fontsize=12)

# Show everything
title = "Comparing Survival functions between Actual and Predicted"
plt.legend(fontsize=12)
plt.title(title, fontsize=15)
plt.ylim(0, 1.05)
plt.show()

PySurvival - CoxPH model - Actual vs Predicted

Figure 3 - Comparing Actual vs Predicted