

The math of Survival Analysis

Now that we have introduced the main notions in Survival Analysis, let's define the variables and functions that we will be using and give simple examples to provide additional insight:

---

$T$, Survival Time

$T$ is a positive random variable representing the waiting time until an event occurs. Its probability density function (p.d.f.) is $f(t)$ and cumulative distribution function (c.d.f.) is given by $$\begin{equation*} F(t) = \text{Pr} \left[ T < t \right] = \int_{-\infty}^{t} f(u) du \end{equation*}$$

• Example: Let's take the example of credit risk and assume that the event of interest is fully repaying a loan. We can now analyze the cumulative distribution function of two distinct borrowers through time.

  Figure 1 - Comparing cumulative distribution functions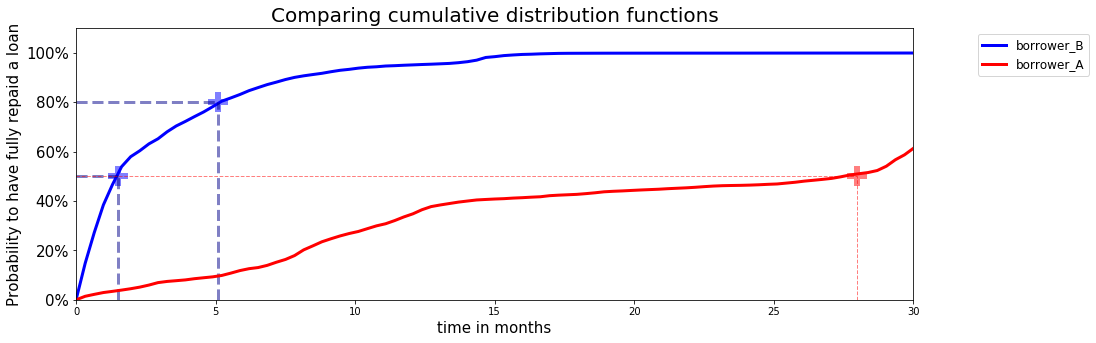

  Here, we can see that the probability that Borrower B has fully repaid his/her loan reaches 50% or 80% much faster than Borrower A's. This indicates that Borrower B is potentially less risky than Borrower A.

---

$S(t, x)$, Survival function

$S(t)$ is the probability that the event of interest has not occurred by some time $t$ $$\begin{equation*} S(t) = 1 - F(t) = \text{Pr} \left[ T \geq t\right] \end{equation*}$$

• Example: Here, we will consider the example of churn modeling, assume that the event of interest is stopping the SaaS subscription and analyze the survival function of three distinct customers through time.

  Figure 2 - Comparing survival functions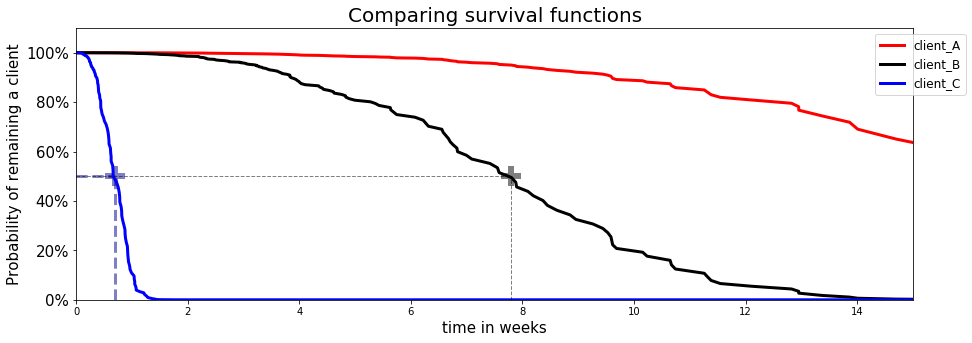

  Here, we can see that the probability of remaining a customer reaches 50% much faster for Client C than Client B. On the other hand, Client A's probability doesn't even go below 60% from week 0 to week 15 of the analysis. In a nutshell,
  • Client C is very likely to churn within the first 2 weeks
  • Client B is likely to churn within the next 15 weeks
  • Client A is very likely to remain a customer within the next 15 weeks.

---

$h(t, x)$, hazard function and $r(x)$ risk score

$h(t)$ expresses the conditional probability that the event will occur within $[t, t+dt)$ , given that it has not occurred before. $$\begin{equation*} h(t) = \lim_{dt \to 0} \frac{\text{Pr} \left[ t \leq T < t + dt\ | T \geq t\right ] }{dt} = \frac{f(t)}{S(t)} = -\frac{d}{dt}\log S(t) \end{equation*}$$

Thus, the hazard and Survival functions are linked by the following formula: $$\begin{equation*} S(t) = \exp\left(- \int_{0}^{t} h(u) du \right) \end{equation*}$$ where $H(t) = \int_{0}^{t} h(u) du$ is the cumulative hazard function

However, the hazard function is rarely used in its original form. Most of the time, we subdivide the time axis in $J$ parts and calculate the risk score of a sample $x$, such that: $$\begin{equation*} r(x) = \sum_{j=1}^J H(t_j, x) \end{equation*}$$

• Example: Let's reuse our churn example. The previous conclusion can be translated into risk scores such that: $r(x_A) < r(x_B) < r(x_C)$. Indeed the faster you experience the event, the higher your risk score is.