Skip to content

Kernel SVM model

The Kernel SVM model available in PySurvival is an adaptation of the work of Sebastian Polsterl et al..

Instance

To create an instance, use pysurvival.models.svm.KernelSVMModel.

Methods

__init__ - Initialization 

KernelSVMModel(kernel = "gaussian", scale=1., offset=0., degree=1.,
    auto_scaler = True)

Parameters:

  • kernel: str (default="gaussian") -- The type of kernel used to fit the model. Here's the list of available kernels:

    • Polynomial
    • Gaussian
    • Exponential
    • Tanh
    • Sigmoid
    • Rational Quadratic
    • Inverse Multiquadratic
    • Multiquadratic

  • scale: float (default=1) -- Scale parameter of the kernel function

  • offset: float (default=0) -- Offset parameter of the kernel function

  • degree: float (default=1) -- Degree parameter of the polynomial/kernel function

fit - Fit the estimator based on the given parameters

fit(X, T, E, with_bias = True, init_method='glorot_normal', lr = 1e-2,
    max_iter = 100, l2_reg = 1e-4, tol = 1e-3, verbose = True)

Parameters:

  • X : array-like -- input samples; where the rows correspond to an individual sample and the columns represent the features (shape=[n_samples, n_features]).

  • T : array-like -- target values describing the time when the event of interest or censoring occurred.

  • E : array-like -- values that indicate if the event of interest occurred i.e.: E[i]=1 corresponds to an event, and E[i] = 0 means censoring, for all i.

  • with_bias: bool (default=True) -- Whether a bias should be added

  • init_method : str (default = 'glorot_uniform') -- Initialization method to use. Here are the possible options:

    • glorot_uniform: Glorot/Xavier uniform initializer
    • he_uniform: He uniform variance scaling initializer
    • uniform: Initializing tensors with uniform (-1, 1) distribution
    • glorot_normal: Glorot normal initializer,
    • he_normal: He normal initializer.
    • normal: Initializing tensors with standard normal distribution
    • ones: Initializing tensors to 1
    • zeros: Initializing tensors to 0
    • orthogonal: Initializing tensors with a orthogonal matrix,

  • lr: float (default=1e-4) -- learning rate used in the optimization

  • max_iter: int (default=100) -- maximum number of iterations in the Newton optimization

  • l2_reg: float (default=1e-4) -- L2 regularization parameter for the model coefficients

  • alpha: float (default=0.95) -- confidence level

  • tol: float (default=1e-3) -- tolerance for stopping criteria

  • verbose: bool (default=True) -- whether or not producing detailed logging about the modeling

Returns:

  • self : object

predict_risk - Predicts the risk score 

predict_risk(x, use_log=True)

Parameters:

  • x : array-like -- input samples; where the rows correspond to an individual sample and the columns represent the features (shape=[n_samples, n_features]). x should not be standardized before, the model will take care of it

  • use_log: bool (default=False) -- whether or not appliying the log function to the risk values

Returns:

  • risk_score: numpy.ndarray -- array-like representing the prediction of the risk score

Example

Let's now see how to use the KernelSVMModel models on a simulation dataset generated from a parametric model.

#### 1 - Importing packages
import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
from pysurvival.models.svm import KernelSVMModel
from pysurvival.models.simulations import SimulationModel
from pysurvival.utils.metrics import concordance_index
from sklearn.model_selection import train_test_split
from scipy.stats.stats import pearsonr
# %pylab inline # to use in jupyter notebooks

#### 2 - Generating the dataset from the parametric model
# Initializing the simulation model
sim = SimulationModel( survival_distribution = 'Log-Logistic',
                       risk_type = 'square',
                       censored_parameter = 1.1,
                       alpha = 1.5, beta = 4)

# Generating N Random samples
N = 1000
dataset = sim.generate_data(num_samples = N, num_features = 4)

# Showing a few data-points
dataset.head(2)

We can now see an overview of the data:

x_1 x_2 x_3 x_4 time event
13.234733 10.0 12.0 11.0 0.264510 1.0
4.694893 14.0 11.0 7.0 0.000026 1.0

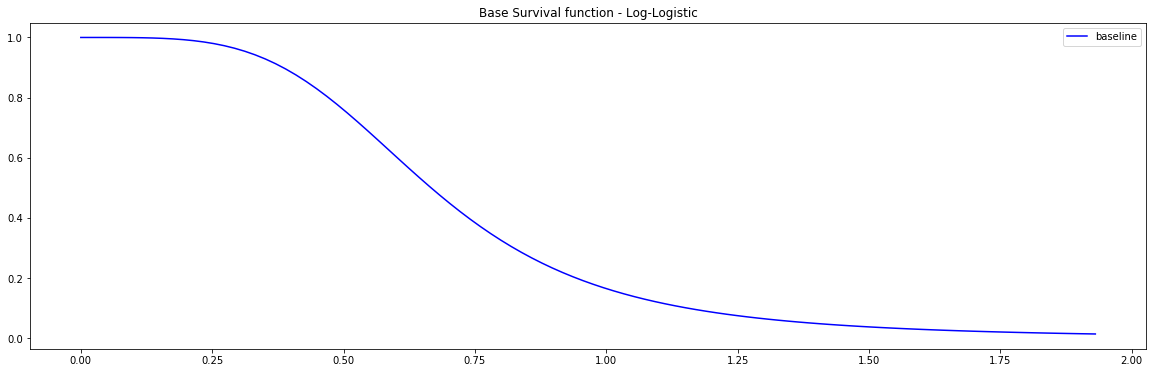
Pysurvival also displays the Base Survival function of the Simulation model: 

from pysurvival.utils.display import display_baseline_simulations
display_baseline_simulations(sim, figure_size=(20, 6))
PySurvival - Kernel SVM - Base Survival function of the Simulation model
Figure 1 - Base Survival function of the Simulation model

#### 3 - Splitting the dataset into training and testing sets
# Defining the features
features = sim.features

# Building training and testing sets #
index_train, index_test = train_test_split( range(N), test_size = 0.2)
data_train = dataset.loc[index_train].reset_index( drop = True )
data_test  = dataset.loc[index_test].reset_index( drop = True )

# Creating the X, T and E input
X_train, X_test = data_train[features], data_test[features]
T_train, T_test = data_train['time'].values, data_test['time'].values
E_train, E_test = data_train['event'].values, data_test['event'].values


#### 4 - Creating an instance of the SurvivalSVM model and fitting the data.
svm_model = KernelSVMModel(kernel='Gaussian', scale=0.25)
svm_model.fit(X_train, T_train, E_train, init_method='orthogonal',
    with_bias = True, lr = 0.8,  tol = 1e-3,  l2_reg = 1e-4)

#### 5 - Cross Validation / Model Performances
c_index = concordance_index(svm_model, X_test, T_test, E_test) #0.89
print('C-index: {:.2f}'.format(c_index))

Because we cannot predict a survival function with KernelSVMModel, let's look at the risk scores and see how correlated they are to the actual risk scores generated from the Simulation model.

#### 6 - Comparing the model predictions to Actual risk score
# Comparing risk scores
svm_risks = svm_model.predict_risk(X_test)
actual_risks = np.log(sim.predict_risk(X_test).flatten())
print("corr={:.4f}, p_value={:.5f}".format(*pearsonr(svm_risks, actual_risks)))
# corr=-0.7519, p_value=0.00000